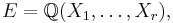Hilbert's irreducibility theorem
In number theory, Hilbert's irreducibility theorem, conceived by David Hilbert, states that every finite number of irreducible polynomials in a finite number of variables and having rational number coefficients admit a common specialization of a proper subset of the variables to rational numbers such that all the polynomials remain irreducible. This theorem is a prominent theorem in number theory.
Contents |
Formulation of the theorem
Hilbert's irreducibility theorem. Let
be irreducible polynomials in the ring
Then there exists an r-tuple of rational numbers (a1,...,ar) such that
are irreducible in the ring
Remarks.
- It follows from the theorem that there are infinitely many r-tuples. In fact the set of all irreducible specialization, called Hilbert set, is large in many senses. For example, this set is Zariski dense in
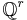
- There are always (infinitely many) integer specializations, i.e., the assertion of the theorem holds even if we demand (a1,...,ar) to be integers.
- There are many Hilbertian fields, i.e., fields satisfying Hilbert's irreducibility theorem. For example, global fields are Hilbertian.
- The irreducible specialization property stated in the theorem is the most general. There are many reductions, e.g., it suffices to take
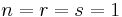 in the definition. A recent result of Bary-Soroker shows that for a field K to be Hilbertian it suffices to consider the case of
in the definition. A recent result of Bary-Soroker shows that for a field K to be Hilbertian it suffices to consider the case of 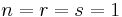 and
and 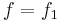 absolutely irreducible, that is, irreducible in the ring Kalg[X,Y], where Kalg is the algebraic closure of K.
absolutely irreducible, that is, irreducible in the ring Kalg[X,Y], where Kalg is the algebraic closure of K.
Applications
Hilbert's irreducibility theorem has numerous applications in number theory and algebra. For example:
- The inverse Galois problem, Hilbert's original motivation. The theorem almost immediately implies that if a finite group G can be realized as the Galois group of a Galois extension N of
-
- then it can be specialized to a Galois extension N0 of the rational numbers with G as its Galois group. (To see this, choose a monic irreducible polynomial f(X1,…,Xn,Y) whose root generates N over E. If f(a1,…,an,Y) is irreducible for some ai, then a root of it will generate the asserted N0.)
- Construction of elliptic curves with large rank.
- Hilbert's irreducibility theorem is used as a step in the Andrew Wiles proof of Fermat's last theorem.
- If a polynomial
![g(x) \in \mathbb{Z}[x]](/2012-wikipedia_en_all_nopic_01_2012/I/7c8fae5582618355ada191d42a47d283.png) is a perfect square for all large integer values of x, then g(x) is the square of a polynomial in
is a perfect square for all large integer values of x, then g(x) is the square of a polynomial in ![\mathbb{Z}[x]](/2012-wikipedia_en_all_nopic_01_2012/I/1720d8ed9c2582abffc3c0685c1ddb77.png) . This follows from Hilbert's irreducibility theorem with
. This follows from Hilbert's irreducibility theorem with 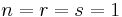 and
and
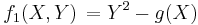 .
.
(More elementary proofs exist.) The same result is true when "square" is replaced by "cube", "fourth power", etc.
Generalizations
It has been reformulated and generalized extensively, by using the language of algebraic geometry. See thin set (Serre).
References
- J. P. Serre, Lectures on The Mordell-Weil Theorem, Vieweg, 1989.
- M. D. Fried and M. Jarden, Field Arithmetic, Springer-Verlag, Berlin, 2005.
- H. Völklein, Groups as Galois Groups, Cambridge University Press, 1996.
- G. Malle and B. H. Matzat, Inverse Galois Theory, Springer, 1999.

![\mathbb{Q}[X_1,\ldots, X_r, Y_1,\ldots, Y_s]. \,](/2012-wikipedia_en_all_nopic_01_2012/I/724e83b99e0628fba44d9c1f90d0310b.png)

![\mathbb{Q}[Y_1,\ldots, Y_s]. \,](/2012-wikipedia_en_all_nopic_01_2012/I/1325ca51292814ccec1410116ddb55fe.png)